矩阵行列式
误区
以前听说行列式按定义计算是超多项式的
不对啊数学课上面(某些人)讲的不是对角线什么的么
今天发现,只有二维世界和三维世界才是这样的,高维世界被无视?
真希望你们自招什么的考个4×4的行列式(笑)
实质
N×N矩阵->标量的函数
写法
det(A) 或 |A|
意义
面积,体积等有向积在多维空间推广
定义
G是1..n的所有置换的集合,g是其中一个置换
sgn(g)定义为(-1)^inv(g),inv(某序列)为序列的逆序对
N×N矩阵A的行列式定义如下
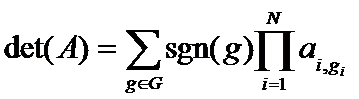
直接使用定义式计算行列式的时间复杂度是超多项式的
性质
1.若A中有某一行或某一列全为0,则det(A)=0
证明 由定义式显然
2.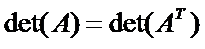
证明 由定义式显然
3.正整数构成的矩阵A,如果存在i和d使得对于所有j in [1..N]有d|a(i,j)
则d|det(A)
证明 由定义式显然
4.行列式某行同乘d,行列式乘d
证明 由定义式显然
5.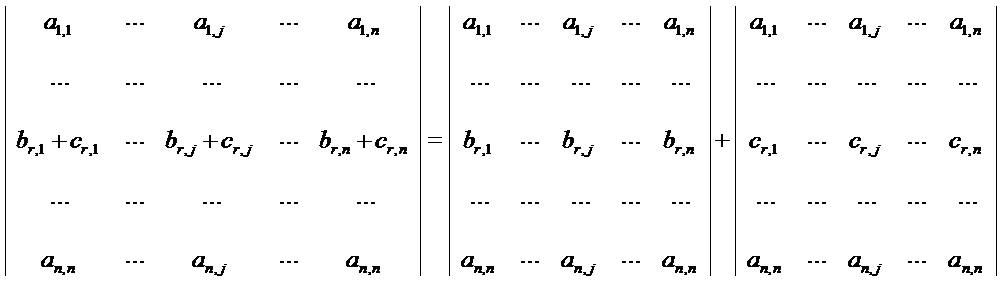
证明 把三个行列式看成矩阵A,B,C
我们需要证明det(A)=det(B)+det(C)
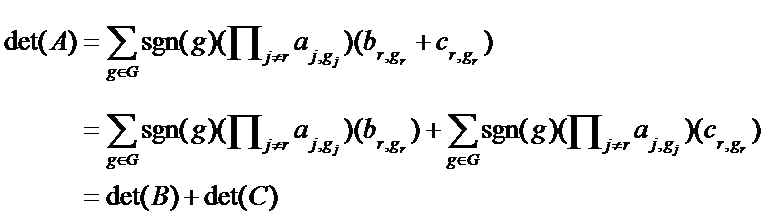
6.行列式两行互换,改变行列式正负符号
证明 互换两行,可以等价地认为就互换了每个置换中那两项
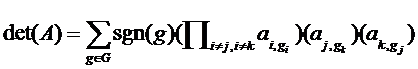
显然等价于交换g(j),g(k),证明交换后置换的逆序对数变化是奇数
考虑与两项前面,中间和后面形成的逆序对,以及两项本身,可得
g(j),g(k)与前面的以及后面的形成逆序对数不变,中间变化是偶数,
g(j),g(k)自己的逆序对数变化1,所以det取反
7.任何A,B有det(AB)=det(A)det(B)
证明 暂时不会
8.若行列式中两行完全相同,行列式值为0
证明 交换之后行列式值取反,但是行列式值没改变.
9.行列式某行加到另一行上面,行列式的值不变
证明 参见性质10的证明
10.行列式某行乘某常数加到令一行上面行列式的值不变
证明 由性质5把行列式拆开,前者为原行列式
后者存在两行,其中一行是另外一行的某常数倍
常数提出来,得到后者存在两行完全相同,行列式值为0
11.行列式中若存在某个线性相关的行集合,行列式值为0
证明 可以通过线性组合,参见上一条性质,使得行列式某行全变为0
12.上下三角矩阵的行列式等于对角线元素积
证明
以上三角矩阵为例,显然要不让a(n,g(n))=0,只能g(n)=n
归纳可得要不让a(i,g(i))=0,只能对任意i有g(i)=i
如果a(i,g(i))那么这个g对于行列式值贡献为0.
算法
1.按照定义计算
2.O(n^3)算法
类似高斯消元把原矩阵转成上下三角矩阵,套用性质11
应用
1.矩阵A非奇异当且仅当det(A)!=0
2.Kirchhoff矩阵树理论,就是生成树计数,参见vfk的Blog.
3.NOI生成树计数
2022年2月04日 17:37
In the case of previous bills where the amount was already paid online but not updated in the BSNL portal system, please visit the nearest cash counter to pay the current bill or pay the total outstanding amount as shown at the quick payment portal, where the excess paid amount will be automatically adjusted in the next coming bill. BSNL online bill payment Check out the new step-by-step approach for fast paying your BSNL bill online without logging in using a credit card, debit card, or internet banking payment.
2023年5月02日 20:07
Outstanding Service! Great Execution of their plans in work! They are just perfect! I would like to recommend them to everyone out there! You will not regret it! drug addiction help
2023年5月22日 19:35
Professional writers have joined together to create PSC Model Papers in order to provide thorough journalistic coverage of current events across the nation (India). Our team consists of professional writers and citizen journalists with a variety of journalism interests who are passionate about disseminating pscmodelpapers.in the news in a transparent manner for the benefit of the general public.Our reporting team aims to produce news for all age groups and provide intimate coverage of recent events to show the real picture. As we want to provide news divided into General, Political, Crime, Sports, Entertainment, Education, and World News, our goal is to meet the needs of people of all age groups.