后缀自动机笔记
本文用丽洁的PPT中的理论(Right集合,状态的min,max)来解释好了.
不过在细节上会和丽洁的有出入,比如蒟蒻太弱了受不了开区间表示.
可能丽洁的理论和程序实现关系不大不过确实能帮助你理解SAM
To I myself
fhq的例子被丽洁的课件中的理论解释,一张比较能代表后缀自动机的图
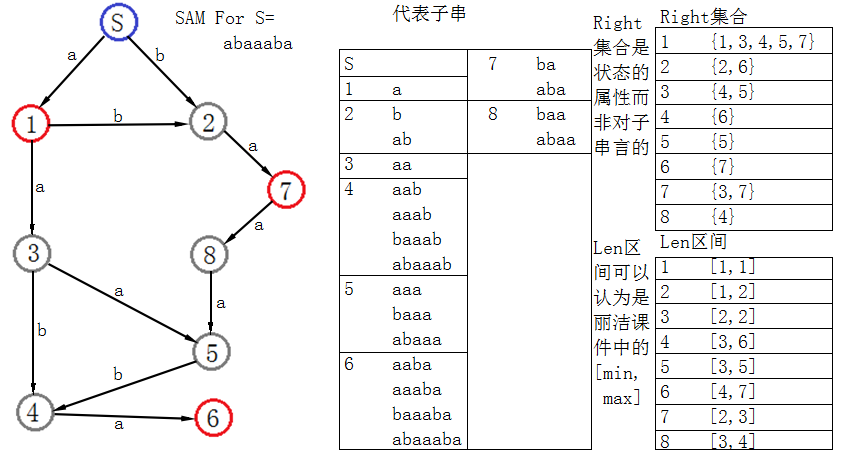
/* (Parent画出来太凌乱了所以没画) */
一 后缀自动机
1.定义
给定串S,S的后缀自动机(SAM)是一个DFA,它接受S的所有后缀
2.暴力的SAM
建立字典树把每个后缀插进去,复杂度最差O(n^2).
下文我们讨论最小状态SAM,并证明其复杂度是线性的
3.性质
S'不是S的子串,则ST(S')=NULL
输入S'之后绝不可能转移到接受态
S'是S的子串,则ST(S')≠NULL
输入S'之后存在可能转移到接受态
b in Reg(ST(a)) <=> ab是S的后缀,暗示着b是S的后缀
Reg(ST(a)) in Suf
若a在S的[l,r]位置出现则ST(a)识别Suffix(r+1)
设a在S的{[li,ri]}位置集合出现
则Right(a)={ri},Reg(ST(a))={Suffix(ri+1)}
若a≠b,a,b in Fac
Right(a)=Right(b) <=> Reg(ST(a))=Reg(ST(b)) <=> ST(a)=ST(b)
这保证了A是最小状态SAM
由上可规定某状态s有自带属性s.R,表示ST(a)=s的所有a的Right(a)
也就是所有Right(a)=s.R的a都会使自动机从初态转移到s
可以说成s代表了所有这样的a
设r' in s.R,具体是哪个没有关系
再给定len就可以确定一个子串a=S[r'-len+1..r']
如果上述子串不由s代表,即Right(a)≠s.R
则定义len关于s非法否则合法
★定理 如果l,r关于s合法则任意m in [l,r]关于s合法
证明
设m in (l,r)且m关于s非法,即a=S[r'-m+1..r'],Right(a)≠s.R
由于m非法,分类讨论
情况1.Right(a)中有s.R中没有的元素
即a在某个r”出现,r”不在s.R中
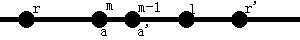
定义a'=S[r'-(m-1)+1..r'],显然a'是a的子串
则Right(a')中也应该也有这个不在s.R中的元素
即a'也在这个r”出现,再归纳法最终可推得l非法,矛盾
情况2.s.R中有Right(a)中没有的元素

类似上述证明可推得r非法,矛盾
☆定理的意义
关于s合法的长度构成连续区间记作[min(s),max(s)]
此处min函数的定义域是自动机的状态所以写成圆括号
★定理 最小状态SAM的状态数是线性的
证明
考虑不同的状态a,b,考虑a.R和b.R
1.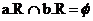
2.否则设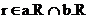
由SAM是DFA可得a,b代表的子串交集为空
易证关于a,b合法的区间交集为空
不妨设max(a)<min(b)

易证a代表的任何子串是b代表的任何子串的后缀
那么对于位置r”
如果b出现于r” 则a出现在r”
如果b不出现在r” 则a不一定不出现在r”
故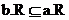 这里是真子集
这里是真子集
故不同的状态a,b只可能
1.a.R,b.R无交集
2.a.R,b.R某一个是另一个真子集
可以认为状态的R形成了一棵树(图参见丽洁课件)
如果有元素不出现在任何叶子中则加一个废结点即可
这样这个树有|S|个叶子,每个非叶结点至少有2个儿子,
按归纳法易得这个树的大小是线性的,而状态数不超过树结点数
故状态数是线性的,以后我们称该树为Parent树
给定状态s,Parent(s)定义为状态t
|t.R|极小且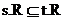 ,也就是s在Parent树中父亲
,也就是s在Parent树中父亲
★定理 max(Parent(s))=min(s)-1
证明
考虑相对s合法的区间l1
相对Parent(s)合法的区间l2
相对Parent(Parent(s))合法的...li
他们互不相交(参见状态数线性的证明)
如果max(Parent(s))<min(s)-1
则易证min(s)-1这长度不关于任何包含s.R的状态合法
则后果是该SAM不识别Suffix(r'-(min(s)-1)+1),r' in s.R,显然荒谬
★定理 最小状态SAM的转移边数是线性的
证明
首先如果trans(a,c)=NULL 该边认为不存在
求出SAM的有向图描述的以init为根的树形图,树边的数量是线性的
考虑非树边 trans(a,c)=b和生成树中路径P init->a-c->b->某接受态
显然P代表某后缀
对于每个后缀都在SAM上走一遍,认为该后缀对应走到的首条非树边
显然这样能走完SAM,故非树边个数不多于后缀数即是线性的
S的任何子串S'都被某确定的状态代表,该状态为ST(S')
对于任何状态s,parent(s)代表的任何子串是s代表的任何子串的后缀
考虑 由于max(parent(s))=min(s)-1
由于max(parent(s))=min(s)-1
在r这个地方该定理成立,一个r成立则所有r成立
4.线性构造SAM
算法思想 增量法
初始化 直接root表示空串,类似Trie的root
假设串T的SAM构造完成,现在加入ch构造串 Tch 的SAM,记L=|T|
新建结点np,np.R={L+1},max(np)=L+1,其是接受态
只有L in s.R的状态s才有被修改的可能
考虑状态p=ST(T),现在p.R={L}
由Parent树可得所有L in s.R的s要不是p就是p的祖先.
设自底向上这些结点是v[1]=p,v[2]..v[k]=root.
考虑v[i],在v[i]后添加一个ch形成nv[i]
vi.R中只有S[ri+1]=ch的ri才合法即
nv[i].R={r'i+1 | (r'i in v[i].R)and(S[r'i+1]=ch) }
如果v[i]没有ch出弧则只有ri=L才是合法的,直接加连向np的ch弧
即trans(v[i],ch)=np
如果v[i]有ch出弧,由于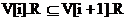 故v[i+1]也一定有
故v[i+1]也一定有
令q=trans(v[i],ch),显然q.R={ (r'i+1 | r'i in v[i].R)and(S[r'i+1]=ch) }
但是我们不一定能直接把L+1加入q.R,反例如下图
蓝色初始态 红色接受态 红弧指向parent 其他都很普通
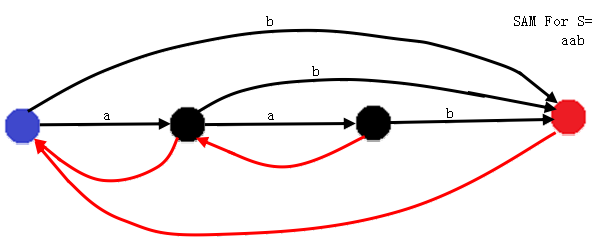
从左到右的R集合为
{1,2,3} {1,2}, {2} {3}
此时T = [aab],加入ch=[b]
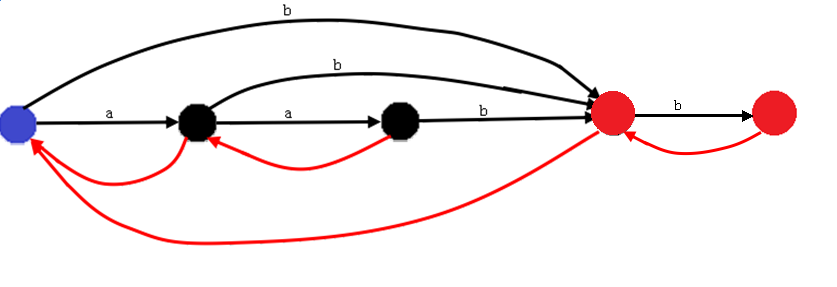
从左到右的R集合为
{1,2,3,4} {1,2} {2} {3,4} {4}
这个是v[i] 这个是q
但是Right(a)={3,4}的a只有[b],这就造成了第三个结点的max减少
或者你可以说是结点代表的子串混乱了.
当然如果max(q)=max(v[i])+1就不会产生这个问题因为
max(trans(v[i],ch))>=max(v[i])+1=max(q)不会造成max(q)减少
而由以下的正确建法便不会产生这个问题
正确建法
对于每个结点维护max域,代表该状态max(s)
维护last指针指向max(s)最大的状态s
每次如下执行算法
S1 新建np代表新结点,np.max=last.max+1,p=last
S2 如果p没有ch出弧,直接连ch出弧到np并且p=p.parent,继续S2
否则转S3
S3 q=trans(p,ch) 如果q.max=p.max+1则np.parent=q否则
新建nq,定义现在对任何ch,trans(nq,ch)=trans(q,ch)
nq.max=p.max+1,nq.parent=q.parent,q.parent=nq,np.parent=nq
从p开始往上的所有指向q的指针指向nq,算法完成
最后特判一下边界
二 后缀自动机的应用
1.最小表示法
给定S,求i使得从i开始的循环S表示字典序最小
对于串SS建立SAM,每次贪心走最小的转移边走完|S|步即可
最后求i可以用KMP
2.字符串匹配
给定模式P,文本T,进行串匹配
建立P的SAM,每次输入T当前位置的字符
如果当前位置有输入字符的转移弧直接转移即可
否则沿Parent指针走到第一个有该转移弧的状态或者根如果没有这样的状态
更新匹配长度.一旦发现匹配长度=|P|报告匹配
或者一旦走到s,s.R={|P|}则报告匹配
这提示我们SAM有一个功能
给出A,B,对于每个i,求出g[i]=max{j | B[i-j+1..i]是A的子串}
具体应用参见CTSC2012 Cheat
3.LCS
给定A,B,求LCS,LCS应该是连续的一段.
直接上上面SAM的功能即可
4.定长不同子串计数
给定S求S有多少个长度为L的不同子串
引用vfk的Hash Killer里面的话
“后缀自动机上代表的长度区间包含L的结点个数”
三 代码
可能"有点"压行
program Suffix_Automaton;
type pnode=^tnode;
tnode=record
max:longint;
pre:pnode;
next:array[1..26] of pnode;
end;
var root,last,null:pnode;
procedure sam_init;
begin
new(null); with null^ do begin
max:=-1; pre:=null; filldword(next,length(next),dword(null));
end;
new(root); with root^ do begin
max:=0; pre:=null; filldword(next,length(next),dword(null));
end; last:=root;
end;
function newnode(imax:longint):pnode;
begin
new(newnode); with newnode^ do begin
max:=imax; pre:=null; filldword(next,length(next),dword(null));
end;
end;
procedure add(ch:byte);
var p,np,q,nq:pnode;
begin
p:=last; np:=newnode(p^.max+1);
while (p<>null)and(p^.next[ch]=null) do begin p^.next[ch]:=np; p:=p^.pre; end;
if p=null then np^.pre:=root else begin q:=p^.next[ch];
if p^.max+1=q^.max then np^.pre:=q else begin
nq:=newnode(p^.max+1); move(q^.next[1],nq^.next[1],sizeof(q^.next));
nq^.pre:=q^.pre; q^.pre:=nq; np^.pre:=nq;
while (p<>null)and(p^.next[ch]=q) do begin p^.next[ch]:=nq; p:=p^.pre; end;
end;
end; last:=np;
end;
begin
end.
2015年8月08日 00:13
最后还是在你这里看懂了,是cljppt很好的补充,谢谢。
2022年3月28日 15:18
The National Stock Exchange has a 15-minute pre-open session that runs from 9:00 a.m. to 9:15 a.m. on all market days except NSE holidays, and the session includes a comparison of order collection and order matching, as well as a 20% price band that is applicable for the National Stock Exchange Pre-Open Session. nse pre open market The order collection period at the National Stock Exchange Pre One will be just 8 minutes, during which time the usual, cancellation, and changes will be available.
2022年9月17日 23:39
History can guide learners to see trends and processes from a broader, holistic perspective and to understand them. Through History, they come into contact with other cultures and societies and in this way they gain a more holistic understanding of the contemporary world and their place in this broader context. Telugu Medium, AP 10th History Model Paper English Medium & Urdu Medium Students of the State Board can download the AP 10th History Model Paper 2023 Pdf with Answers designed based on the revised syllabus and curriculum of the course. Class teachers and leading institutional experts are designed and suggested the Part-A, Part-B, Part-C, and Part-D exams like SA-1, SA-2, FA-1, FA-2, FA-3, FA-4 along with Assignments.
2024年1月13日 23:37
We need many stories, Like genuinely appreciated, You want addiitional data over it, mainly because it can be reasonably exceptional., Take care exclusively for declaring